排序算法

1. 什么是排序

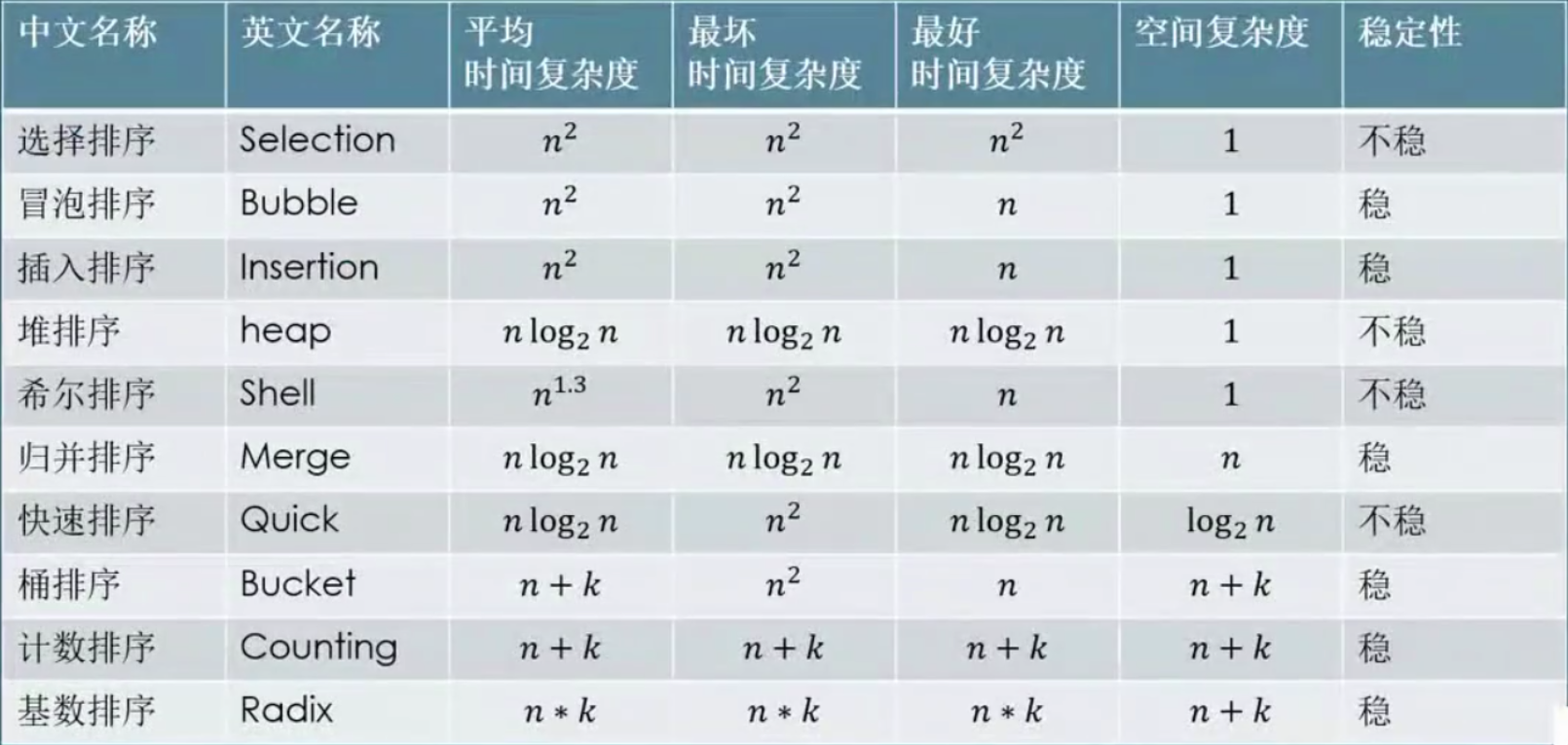
一般情况下最坏，最好时间复杂度，空间复杂度理解记忆
重要：插入，堆，归并，快速

宋词记忆法

选泡插，（选择，冒泡，插入）
快归堆希统计基，（快速，归并，堆，希尔，桶，计数，基数）
N方N老N一三，（选泡插时间复杂度为N²，快归堆时间复杂度为NlogN，希尔排序时间复杂度为N¹.³）
对N加KN乘K，（桶排序，计数排序时间复杂度为N+K，基数排序时间复杂度为N*K）
不稳稳稳不稳稳，（依次的稳定性）
不稳不稳稳稳稳！

2. 选择排序

• 最简单，但是最没用（时间复杂度高，不稳定）
• 算法思想：多次遍历数组，每次都找到最小的数放到最前面。

function selectionSort(arr) {
  let len = arr.length;
  let minIndex, temp;
  for (let i = 0; i < len - 1; i++) {
    minIndex = i; //假设第一个元素是最小的
    for (let j = i + 1; j < len; j++) {
      if (arr[j] < arr[minIndex]) { //找到最小的值
        minIndex = j; //将最小的值的索引保存
      }
    }
    temp = arr[i]; //将最小的值与第一个元素交换
    arr[i] = arr[minIndex];
    arr[minIndex] = temp;
  }
  return arr;
}

3. 冒泡排序

• 简单，但是慢（时间复杂度高，稳定）
• 思路：每次遍历将最大的数移到末尾
• 复杂度分析：第一次迭代需要比较的次数为N次，第二次迭代为N-1次，依次类推，复杂度为 N+(N-1)+(N-2)+……+1 = N(N-1)/2 = O(N²)

function bubbleSort(arr) {
  let len = arr.length;
  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - 1 - i; j++) {
      if (arr[j] > arr[j + 1]) {
        let temp = arr[j];
        arr[j] = arr[j + 1];
        arr[j + 1] = temp;
      }
    }
  }
  return arr;
}

4. 插入排序

• 简单，但是慢（时间复杂度高，稳定）
• 思路：把待排序的记录按其关键码值的大小逐个插入到一个已经排好序的有序序列中，直到所有的记录插入完为止，得到一个新的有序序列。

function insertionSort(arr) {
  let len = arr.length;
  let preIndex, current;
  for (let i = 1; i < len; i++) {
    preIndex = i - 1; //前一个元素的索引
    current = arr[i]; //当前元素
    while (preIndex >= 0 && arr[preIndex] > current) { //前一个元素大于当前元素
      arr[preIndex + 1] = arr[preIndex]; //将前一个元素后移
      preIndex--; //索引前移
    }
    arr[preIndex + 1] = current; //将当前元素插入到合适的位置
  }
  return arr;
}
let arr = [1, 99, 3, 63, 5];
console.log(insertionSort(arr));

5. 简单排序算法总结

• 冒泡排序：基本不用，太慢
• 选择排序：基本不用，不稳定
• 插入排序：样本小，基本有序的时候效率比较高，三种排序中最快的，常用。

6. 快速排序

• 常用（时间复杂度低，不稳定）
• 思想：
  1. 先从数列中取出一个数作为基准
  2. 分区，该数左边的都比该数小，右边的都比该数大
  3. 再对左右区间递归第二步

function quickSort(arr) {
  if (arr.length <= 1) { //如果数组长度小于等于1，直接返回
    return arr;
  }
  let pivotIndex = Math.floor(arr.length / 2); //取中间的值作为基准
  let pivot = arr.splice(pivotIndex, 1)[0]; //取出基准值
  let left = [];
  let right = [];
  for (let i = 0; i < arr.length; i++) {
    if (arr[i] < pivot) { //比基准值小的放左边
      left.push(arr[i]);
    } else { //比基准值大的放右边
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat([pivot], quickSort(right)); //递归调用
}

7. 归并排序

• 常用（时间复杂度低，稳定）
• 思想：分治，将数据化成logN层级，每一层用O（N）的复杂度去解决
  1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
  2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置
  3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
  4. 重复步骤3直到某一指针超出序列尾，将另一序列剩下的所有元素直接复制到合并序列尾

function mergeSort(arr) {
  let len = arr.length;
  if (len < 2) { //如果数组长度小于2，直接返回
    return arr;
  }
  let middle = Math.floor(len / 2); //取中间的值
  let left = arr.slice(0, middle); //取左边的值
  let right = arr.slice(middle); //取右边的值
  return merge(mergeSort(left), mergeSort(right)); //递归调用
}
function merge(left, right) {
  let result = [];
  while (left.length && right.length) { //左右两边都有值
    if (left[0] <= right[0]) { //左边的值小于等于右边的值
      result.push(left.shift()); //将左边的值放入结果数组
    } else { //左边的值大于右边的值
      result.push(right.shift()); //将右边的值放入结果数组
    }
  }
  while (left.length) { //左边还有值
    result.push(left.shift()); //将左边的值放入结果数组
  }
  while (right.length) { //右边还有值
    result.push(right.shift()); //将右边的值放入结果数组
  }
  return result;
}

8. 堆排序

• 常用（时间复杂度低，不稳定）
• 思想：首先建立一个堆，然后不断地比较非叶子节点和堆顶元素的大小，同时调整堆，完成对元素的排序。
  堆排序主要用于动态数据的维护，如在1000000个元素中选出前100名这种N个元素中选出前M个元素的问题，用堆排序最好解决，其复杂度为NlogM

function heapSort(arr) {
  let len = arr.length;
  let i = Math.floor(len / 2 - 1); //取中间的值
  let k = len - 1;
  while (i >= 0) { //从中间开始调整
    heapify(arr, i, len);
    i--;
  }
  while (k >= 0) { //将堆顶元素与最后一个元素交换
    swap(arr, 0, k);
    heapify(arr, 0, k);
    k--;
  }
  return arr;
}
function heapify(arr, i, len) {
  let left = 2 * i + 1; //左子节点
  let right = 2 * i + 2; //右子节点
  let largest = i; //最大值
  if (left < len && arr[left] > arr[largest]) { //左子节点大于最大值
    largest = left;
  }
  if (right < len && arr[right] > arr[largest]) { //右子节点大于最大值
    largest = right;
  }
  if (largest !== i) { //如果最大值不是父节点
    swap(arr, i, largest);
    heapify(arr, largest, len); //递归调用
  }
}
function swap(arr, i, j) {
  let temp = arr[i];
  arr[i] = arr[j];
  arr[j] = temp;
}